
| Home |
Mechatronics |
About RMS |
DMC Sub |
Audio Design |
Education |
Kits & Parts |
Large motional feedback system
- Introduction, requirements and system overview
- Power supply
- Input circuit
- Active cross-over filter unit
- LF amplifier with motional feedback
- MF amplifier with special distortion cancellation
- HF MOSFET amplifier with soft clipping
- Protections
MF amplifier with special distortion cancellation:
The MF amplifier for the midrange driver is designed with focus on low distortion rather than speed with a maximum power level at 1% distortion of 200W. The distortion is reduced by a combination of several measures. First of all operational amplifiers are used at the input with almost unmeasurably low distortion levels. Secondly the signal is first-order filtered to below 20 kHz, preventing distortion products due to HF glitches and latching. Third and most important is the use of a full balanced circuit that applies the principle of "addition of the missing part". In short this principle measures the distortion of one stage in an amplifier and feeds that into another part of the amplifier that can more easily handle the errors. Several configurations exist of this principle where for instance a fast but less powerful power output stage is combined in parallel with a slow but powerful second stage. The current dumping technology from Peter Walker of Quad is a variation on this principle but also in professional mechatronic equipment this principle is used to correct errors that occur in one system by means of a fast and accurate other system.
One problem with this principle in power amplifiers is the need to add signals at relatively high power levels. In the Quad current dumping system this was done by using current-source transconductance amplifiers where the output currents can be added. While current-source power amplifiers are most common in position control for high-tech systems, these amplifiers are unfortunately less favourable in audio because of the low dampingfactor of drivers, especially when a low amount of feedback is applied.
A much better solution to the problem of adding power signals is to apply a dual-ended, so called bridged amplifier where the driver is connected between the outputs of two power amplifiers of which the signals are sign-inverted in respect to each other. This principle was the subject of the Ir (Msc) thesis in 1977 of Hay Kockelmans, presently known from Hai-End Audio in Venlo, that I obtained at Philips where his Msc work was done. The thesis (in Dutch) is available at the archives of the Technical University Eindhoven via this link.
The execution with a full-balanced bridge configuration has several advantages for audio. Firstly the addition is done with voltages, enabling the use of "normal" voltage-source power amplifiers. Secondly it enables a full-balanced system under the condition that two equal amplifiers are used where one amplifier receives the error of the other and vice versa. Although in that case there is not an element that is faster or more powerful than the other the principle still is valid for the same reasons that explain the cause of non-linear distortion.
It is well known that a fully symmetric single-ended power amplifier is not possible to make. In case one uses complementary devices with NPN and PNP transistors or N- and P- channel MOSFETs the difference in majority carriers (electrons or holes) causes an asymmetry in the behaviour of the positive and negative signal part, especially regarding speed during cross-over. The unique use of N-type transistors will create a real asymmetry with a difference in output impedance for both halves of the signal.
In principle a real symmetric analogue output can only be realised by means of a bridged, dual-ended amplifier where the positive signal current passes identical active components in the same current direction as the negative signal current. A special execution of this principle is the circlotron which is essentially a bridged configuration with floating power supplies. When floating power supplies are not preferred, for instance because of the capacitive coupling via the power supply transformer, a symmetric configuration can only be made by using two single-ended amplifiers in a bridge as shown in a simple form below where the driver is connected from A to B.
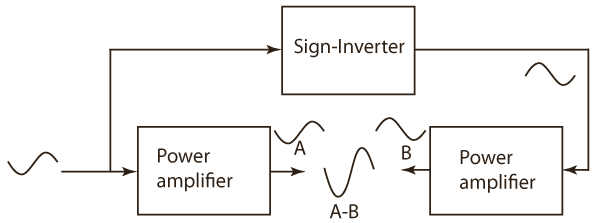
Still, even with a bridged configuration, the cross-over region from negative to positive voltage can give problems as the combined behaviour is determined by the summation of the dynamic behaviour of the two amplifiers. This is explained a follows. The output voltages of both power amplifiers are in principle 180o out of phase. This means that at a zero crossing one of the amplifiers will cross from a negative to a positive voltage while the other crosses in the other direction. When the negative half of one amplifier is slower than its positive half this will result in a small cross-over distortion for the combined signal, even if the other half is fast enough.
This can of course be solved by applying a class-A amplifier or a class AB amplifier with a high idle current but as a less power consuming alternative the principle of "addition of the missing part" can be used to make the fast half of one amplifier compensate the errors by the slow half of the other amplifier. The error will be noticed at a cross-over in the negative direction by the distortion measurement device and this error will be fed to the other amplifier that is crossing from negative to positive, which is much faster.
This is just an example but in the previously referenced Msc thesis it is proven mathematically that this principle cancels distortion....at least when certain conditions are met: The power amplifiers must always have at least some gain, the controlling operational amplifiers need to have no distortion and the loop gains and dynamics need to comply with the general constraints on stability. As will be shown in the LF power amplifier this principle can even correct a large non-linearity around cross-over at low frequencies when a pure class B amplifier is used with only very little idle current.
In the MF-amplifier that is presented on this page, integrated power amplifiers are used that were long ago made bij Philips Semiconductors with acceptable but not great audio properties. The distortion correction principle is able to make them behave far better in the frequency range of interest.
With below circuit diagram the working principle will be further explained.
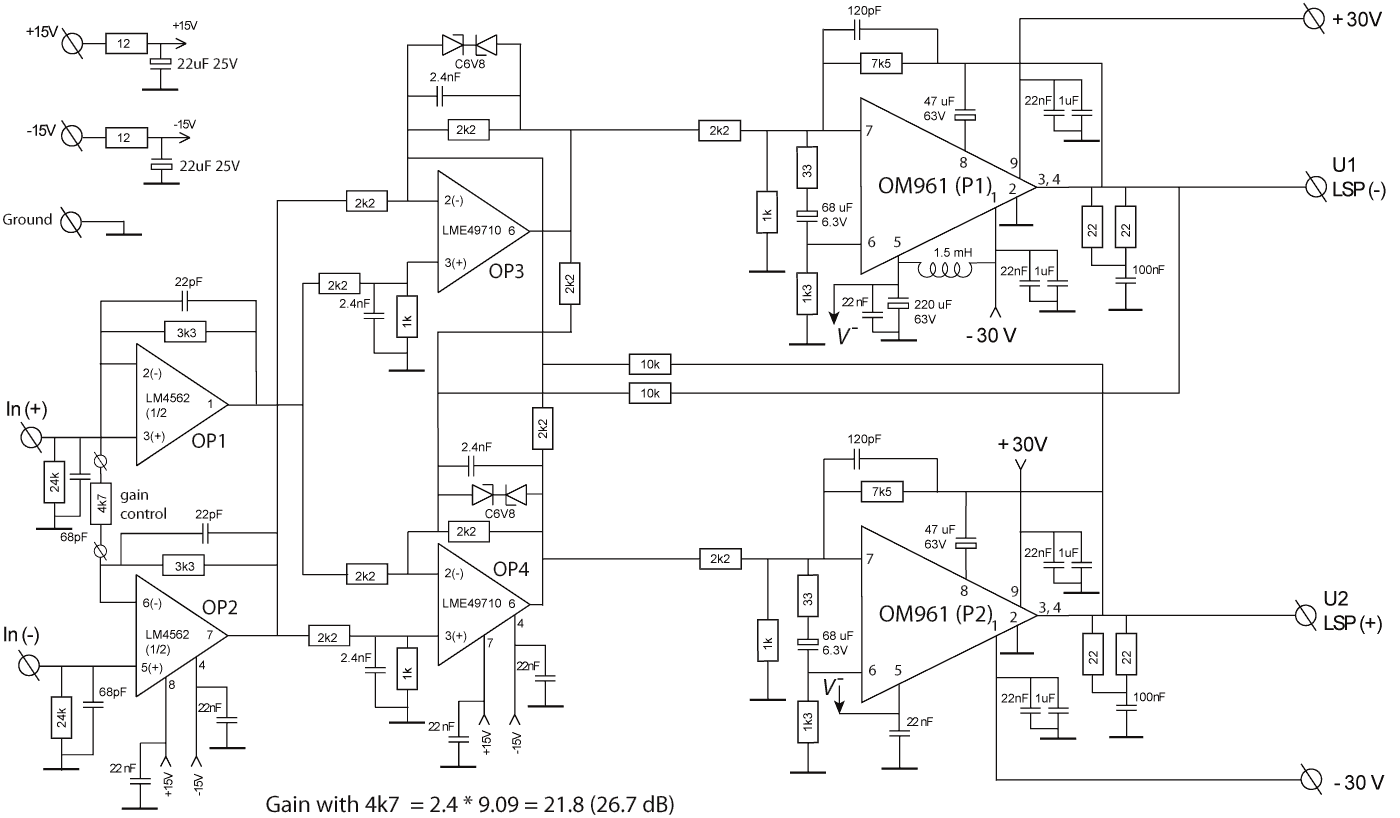
The input signal is fed into a true differential input stage with two operational amplifiers (OP1 and OP2) according to the basic principles of an instrumentation amplifier. Even with a single-ended input signal this method improves the common-mode rejection ratio of the total amplifier, which is needed when combined with different amplifiers on a common ground.
Different from an instrumentation amplifier is the next stage that consists of two sign-inverted differential amplifiers (OP3 and OP4). Without the coupling signals for the "addition of the missing part", these two amplifiers would provide an amplified version of the differential input signal between their outputs with a gain of 2.4. The output of OP3 and OP4 is then fed respectively into the two integrated power amplifiers P1 and P2. The loop-gain of these amplifiers is reduced on purpose by a 33 Ohm resistor in series with a large capacitor between the two inputs in order to limit latch-up effects inside the power amplifiers when clipping occurs. The resulting increase in distortion is fully compensated by the correction principle.The 7k5 feedback resistor with the 2k2 input resistor also implies a smaller closed-loop gain of about 3 than ideal but that is also corrected to the required value of 4.5 by the 10k/2.2k ratio of the correction network. Note that these not so logical resistor values were determined in a previous version of the amplifier that needed a lower gain. It was sufficient to ncrease of the gain later by means of the compensation network.
That being said it is time to better explain the correction network. When starting with OP3, the node at its minus input receives both the current from the signal input from OP2 and the combined current signals from both the output of OP4 and the sign-inverted output of P2. Only in case these two signals differ exactly in magnitude in a ratio of 10/2.2 as determined by the 10k and 2k2 resistors, there would be no resulting current inserted in the node at the minus input of OP3 by the lower power section. Any deviation from that ratio will however lead to an additional current in the minus node of OP3 with a resulting voltage at its output. This additional voltage results in a voltage at the output of P1 that is exactly equal to the missing part from P2.
Even without reading the extensive thesis of Hai Kockelmans this can be checked as follows for an example situation: Assume P1 amplifies exactly with the ïdeal factor 10/2.2=4.545454... and P2 amplifies with the factor 7.5/2.2=3.409090...from the circuit diagram, which represents an error of 1.136363..... When for instance a 1V AC signal of 1 kHz is present at the output of OP4, the output of P2 will be -3.40909... V. The current into the node of OP3 will then be 1/2.2-3.40909.../10=0.1136363... mA, equal to the value of the gain error!. This current gives a voltage of 0.25V over the feedback resistor of 2k2. This voltage will be amplified by P1 into -0.25×10/2.2=-1.13636...V, which is again equal to the difference between the ideal and the erroneous output voltage of P2 for an input voltage of 1 V. Combined both signals add to the ideal voltage.
This same reasoning can be made when P1 is not ideal and its error is compensated by P2. In fact a strange situation happens in the above circuit diagram. Due to the fact that both amplifiers have a gain lower than the ideal value they will not directly compensate the error of the other via above reasoning as their compensation is also affected by the difference in gain. This is however in its turn compensated because also the reaction of the power amplifiers on the compensation signals is measured and compensated, leading ultimately to full compensation. It is clear that such reasoning becomes questionable and it is much better to prove it with mathematics as is done in the thesis of Hai Kockelmans.
An important remark on the application of the principle of addition of the missing part: The reader will wonder why this principle seems to be no longer applied in audio. There are several reasons for that true observation. First of all the use of Power MOSFETs has reduced the need for compensation because of their high speed. Furthermore the high cost of double output stages is not favourable, especially while all these circuits require protection means and high power resistors. Also it is recognised that low non-linear harmonic distortion is less important for the perception of sound quality than low levels of more "dynamic" distortions like transient intermodulation distortion (TIM) and clipping latch-up, while this compensation principle can increase these distortions when not executed well. The limitation to frequencies below 2.5 kHz, as done in this active loudspeaker system with clipping limitation by the zener diodes over OP3 and OP4, avoids these problems sufficiently. Finally with switched-mode class-D amplifiers the asymmetry is solved by applying an identical floating switching control circuit for the gates of the N-channel MOSFETs on both the negative and positive half of the signal.
© 2021 Rob Munnig Schmidt